上下界网络流
前言
在一般的网络流问题中,每条边都有一定的容量,也就是流量上限。而有的问题中,每条边还需要限制一个“流量下限”,也就是流过这条边的流量必须大于等于流量上限且小于等于流量下限。这样的问题需要新的思路来解决,我们需要将其转换为朴素的最大流。
上下界网络流分为几个问题:无源汇上下界可行流、有源汇上下界可行流、有源汇上下界最大流与有源汇上下界最小流。
无源汇上下界可行流
我们知道上下界网络流问题中每条边都有流量下限,所以是不是可以将最小流量流满,然后再跑最大流?显然不行,因为将最小流量流满后的图不一定满足流量守恒,也就是一个点流入的流量等于流出的流量(除源点、汇点)。如下图:
这个图就会变成下面两个图,第一幅是流满最小流量的图,第二幅是剩下最大流量的图。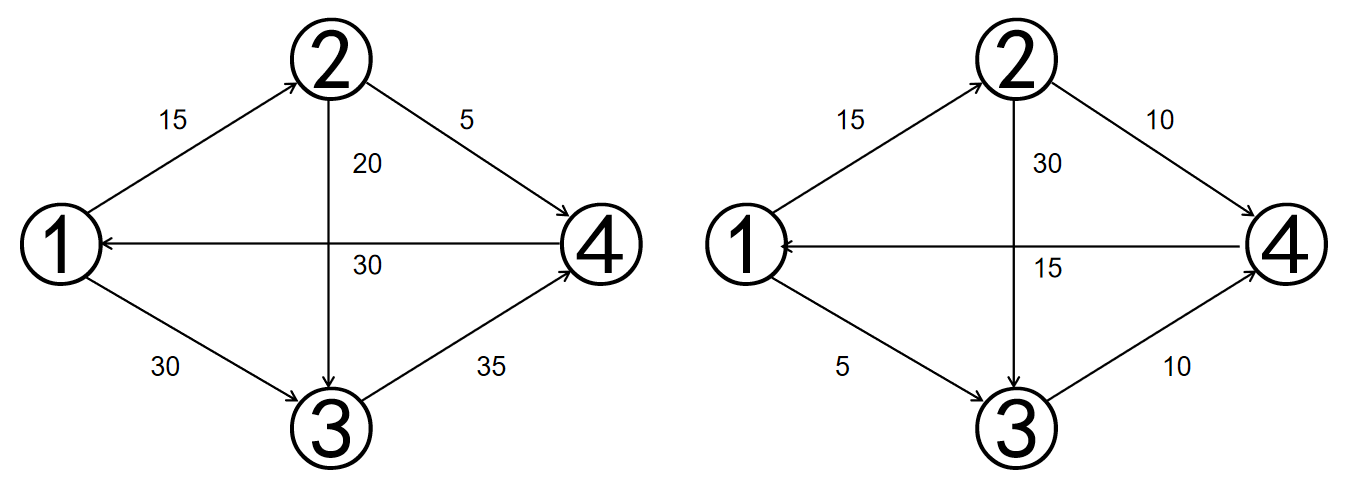
显然,第一幅图并不满足流量守恒,这样第二幅图跑出来了原图也不一定有解。第一幅图中 $1$ 号点流入流量比流出流量少了 $15$,$2$ 号点流入流量比流出流量少了 $10$,$3$ 号点流入流量比流出流量多了 $15$,$4$ 号点流入流量比流出流量多了 $10$。多的流量去哪里,少的流量从哪里来?我们可以用新建的超级源点和超级汇点,用源点补充少的流量,汇点吸走多的流量,如果这个点流入流量较多就连一条边到汇点,这个点流出流量较多从源点向这个点连一条边。但是超级源点和汇点并不存在,流量也不能这样流。所以源点补充的流量应该从第二幅图中来,汇点多出的流量也应该流到第二幅图中去。所以我们在第二幅图中也建立超级源点和汇点,并像第一幅图一样连边,只不过附加边方向反向,超级源点和超级汇点互换。如下图:

如何判断是否存在可行流?我们只需要在第二幅图中从源点到汇点跑最大流,如果从源点流出的按所有边已经流满,也就是流入汇点的所有边都流满了,就说明存在可行流。因为这样就说明第二幅图可以提供第一幅图的超级源点和超级汇点需要的流量,反之则无法满足第一幅图的超级源汇点所需流量,原图也就不存在可行流。由于从源点流出的边的总容量和流入汇点的边的总容量相等,所以只需要判断一边即可。上图就不存在可行流。
有源汇上下界可行流
如果我们在上图把 $1$ 号点设为源点,$4$ 号点设为汇点,情况就又不一样了。源点和汇点的特点是源点可以流出无限流量,汇点可以接收无限流量,源点流出的流量和汇点流入的流量相等。如何实现?我们只需要从汇点向源点连一条容量为无穷的边,就可以保证源点和汇点的流量相等。注意这条容量为正无穷的边是在建立了超级源点与超级汇点之后建立的,不影响与超级源点和超级汇点的连边。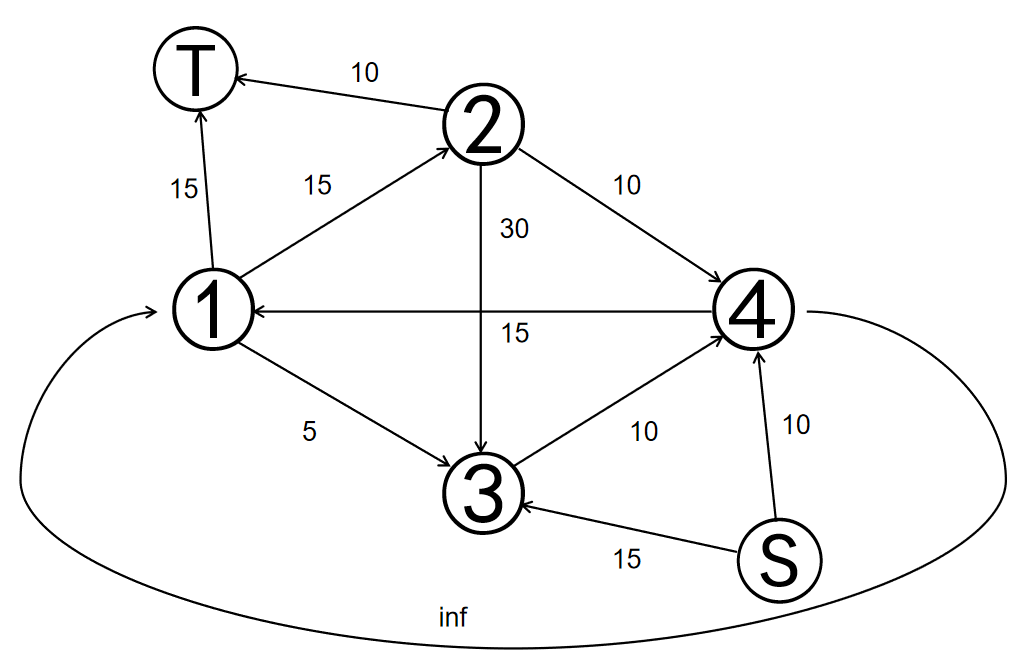
判断方法同上无源汇上下界可行流。这样我们就可以发现原图有解了。从源点流出或汇点流入的流量就是从源点流向汇点的流量。
有源汇上下界最大流
我们现在这个图中跑一边有源汇上下界可行流,找到从汇点到源点的附加边的实际流量,也就是这条边反向边的容量。但是我们只能得到一个可行流,并不是最大流,所以我们要再在残留网络上从源点到汇点跑一边最大流,注意这时要先删去附加边。跑出来的最大流加上原来附加边的实际流量就是最大流。
我们可以发现图中汇点到源点除了附加边,还有一条容量为 $15$ 的边,则就导致可能有流量从汇点到源点的部分流量这种边流过,我们也就无法得到真实的可行流的流量,但是这个对于最后的最大流没有影响,因为如果有流量从这些边流到源点,跑最大流的时候也一定能沿着反向边流过相同的流量到达终点,最后的和就没有变化。
code
1 |
|